A new platform classification

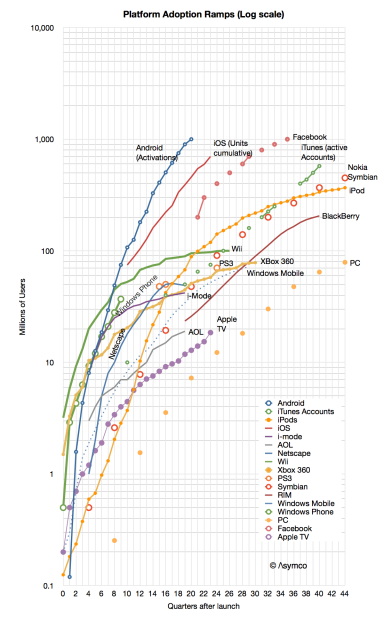
When looking at the Race to a Billion data I noticed that some platform adoption ramps look quite different from others. It’s not just a matter of “slope” or rate of growth but a distinctly different shape.

If you look at the graph below you might see the difference yourself.

First, note that the graph is logarithmic. A straight line on a log chart implies exponential growth (the y values are a constant to the power of the x value). However, none of the graphs show straight lines. None of the platforms follow exponential growth1.

Second, we can eliminate linear or logarithmic functions. They simply do not fit.

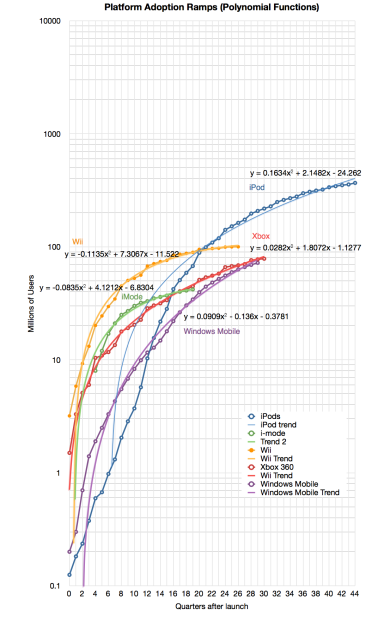
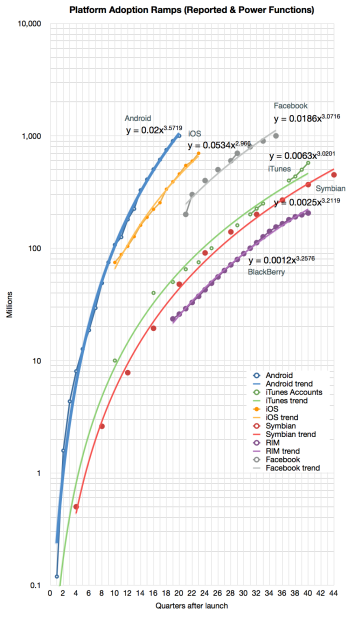
That leaves: polynomial or power. It’s easy to test these alternatives for all the functions and it becomes clear that most of the platforms split into one of these two classes.

Here are the classes2:

Note that I added the formulas for the selected platforms.

I named these classes after their function types: “Power platforms” or “Second Order platforms”3.

This classification has two benefits:

1. It allows a clearer distinction in scope. Both may exhibit signs of network effects, but Power platforms seem to exhibit “global” or unlimited reach while Second Order platforms may have a strong upper bound on reach.
2. It allows more reliable forecasting. If a platform classifies as Power, the forecast could be created with fewer data points.
3. It allows us to guess at the causes of entry into each class for any potential platform challenger.

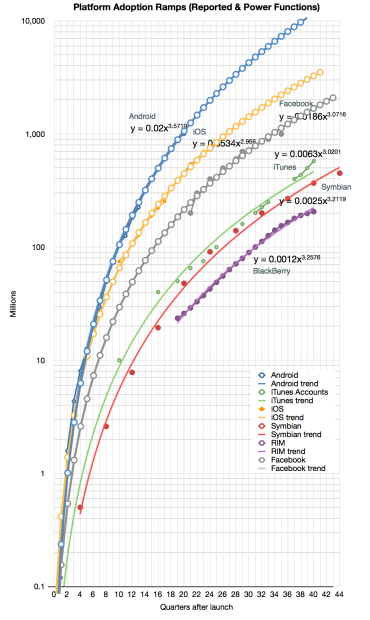
To illustrate the second benefit, I took the Android, iOS and Facebook power functions and modeled (i.e. extrapolated) them for a few quarters into the future. The result is shown below:

The forecast shows the following:

• Android will reach 10 billion activations 10 years after its release (mid 2018)
• iOS will reach 1 billion units sold by end of next year and 3 billion units by its 10th anniversary in 2017.
• Facebook will reach 2 billion users by 2015 after the end of its 10th year.

1. Except perhaps in the very early periods [↩]
2. Some of the platforms had to be dropped because there was no easy fit. My observation is that some of these platforms went through some crisis or change in strategy during their history which caused the pattern of growth to change [↩]
3. Note that all Polynomial functions found above are second order [↩]