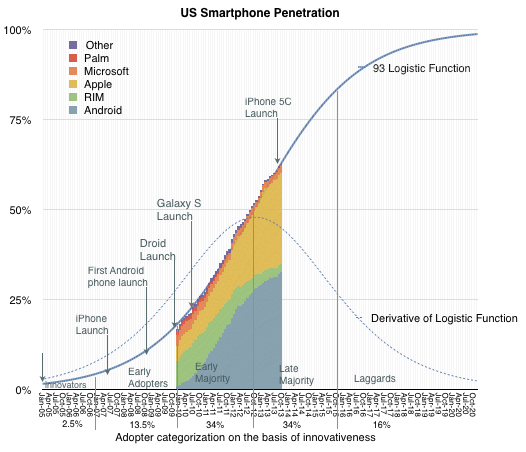
The latest comScore US smartphone survey showing three months’ ending October data has been released and there were no surprises. Smartphone penetration grew to 62.5% representing 149.2 million users. I made a slight adjustment to the predictive logistic function parameters (p1 = 93, p2 = 22.5).
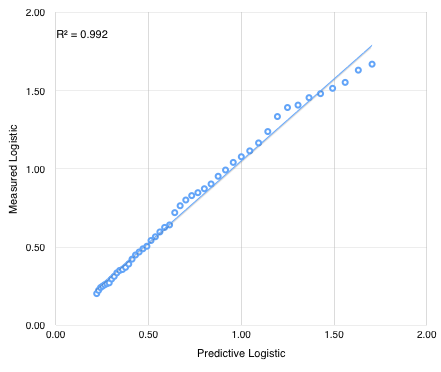
The correlation between predictive and actual logistic function (P/(1-P)) is shown below.
90% penetration (P/(1-P) = 9.23) is now expected by December 2016 when about 230 million users will be using smartphones in the US.
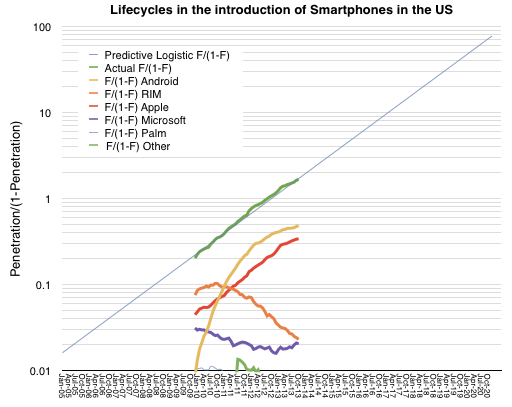
Individual platforms adoption curves are shown as colored areas above and as lines on a logistic plot below:
The parallel behavior of iPhone and the overall market remains unchanged.
Discover more from Asymco
Subscribe to get the latest posts sent to your email.