Seeing What’s Next

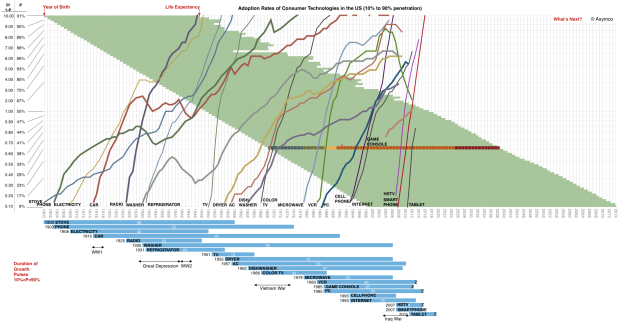
The adoption of smartphones in the US is on track for reaching 90% of the available audience by August 2016. This is a mere eight years after smartphones reached 10% penetration. As far as technologies go, that’s pretty fast. To get an idea of how rapid, I plotted a few other technologies and the time they took to grow within the US market.

A few things to note:

1. The time scale has a yearly resolution spanning 1900 to 2074
2. The penetration scale is logarithmic and shows the ratio of Penetration/(1-Penetration) allowing a linear view of logistic growth.
3. The blue bars summarize the growth pulses and give a starting year and duration in years.
4. Note some traumatic events are marked on the time frame. They partly explain innovation gaps or decreases in adoption.
5. The life expectancy of Americans born from 1900 to 1998 is also shown as green bars. This allows the reader to trace which technologies emerged during the lifetimes of people they might have living memories of. I overlaid one specific lifetime beginning in 1968 and color coded with Childhood, Adolescence, Higher Education, Work live and Retirement as a guide. You can note how the PC emerged when that person would have been in college.
6. Some technologies have not yet saturated and may never do so. They are marked with a “Z” on the bar graph. It might be instructive to understand why.

You’ll also note that the time frame does not end today but that the technology curves do. The time frame includes the expected lifespan of someone born in 1998.

What will they see?

There is a lack of visibility or certainty among observers that anything worthy of inclusion on this graph will ever emerge.

And yet, when glancing at this graph, it would seem that the addressable market, the rate of introduction of new technologies and the speed of adoption have all increased. The area to the right of 2013 looks inviting to a plot of many lines.

Indeed, for the canvas to remain blank would be the riskiest of bets.

What would you put upon it?